The World Leader in Deploying Large AI Models on CPUs

Build and scale Generative AI applications on CPUs
Get superior price performance on CPU-only infrastructure
Maintain privacy and full control of your models and data
Unlock the benefits of Large Language Models with NuPIC™
Whether you’re deploying LLMs for the first time or running in production today, the Numenta Platform for Intelligent Computing (NuPIC) is designed to be efficient, scalable, and secure. No GPUs required!
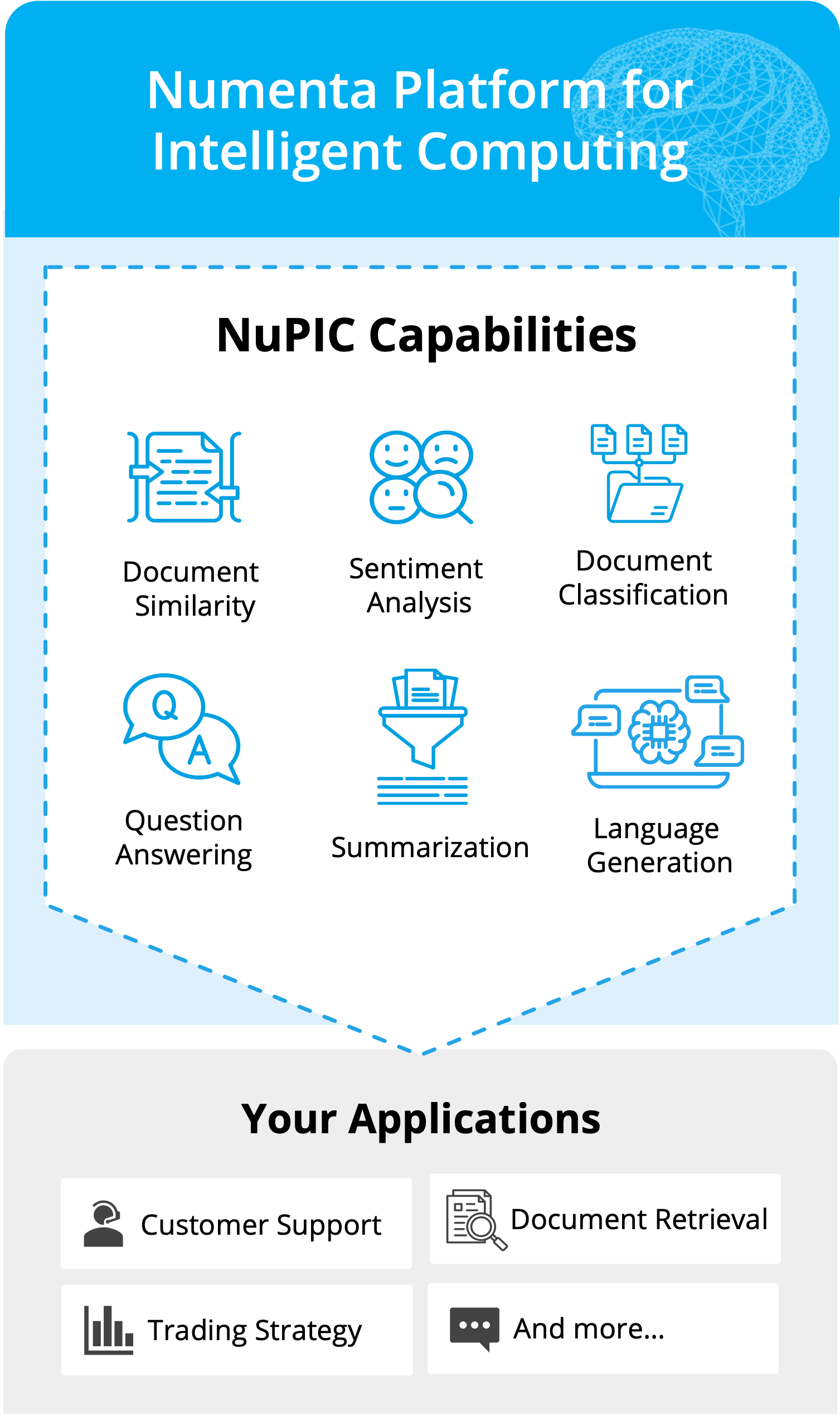
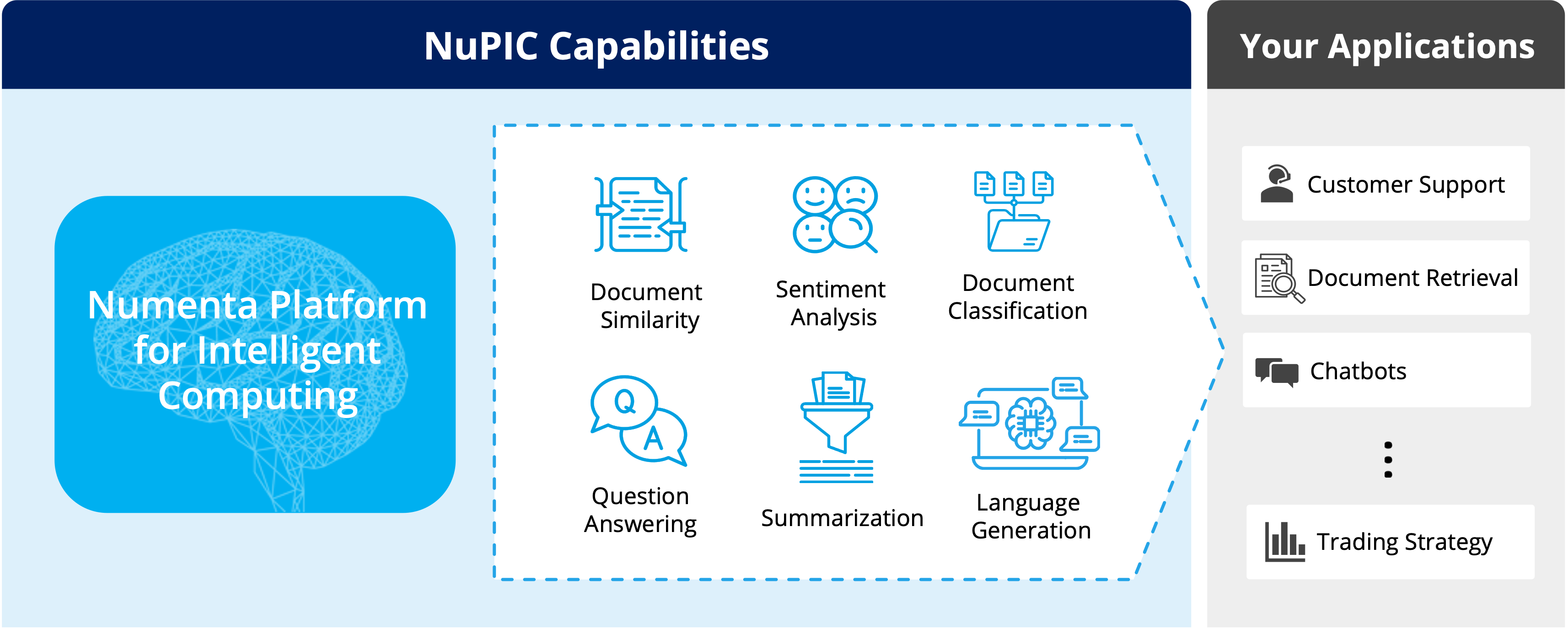
Experience uncompromised speed and flexibility on CPUs
Optimal performance
Ideal for real-time applications
Multi-tenancy
Run hundreds of models on the same server
Effortless scaling
Easily scale CPU-only systems
Simplified MLOps
Easy infrastructure management


Rooted in two decades of deep neuroscience research
Numenta is driven by a mission to deeply understand the brain and apply that understanding to AI. Through mapping our neuroscience-based advances to modern CPU architectures, we are redefining what’s possible in AI. Working with partners like Intel, we are driving AI into the future.
Case Studies

Boosting accuracy without compromising performance: Getting the most out of your LLMs
With our neuroscience-based optimization techniques, we shift the model accuracy scaling laws such that at a fixed cost, or a given performance level, our models achieve higher accuracies than their standard counterparts.

20x inference acceleration for long sequence length tasks on Intel Xeon Max Series CPUs
Numenta technologies running on the Intel 4th Gen Xeon Max Series CPU enables unparalleled performance speedups for longer sequence length tasks.

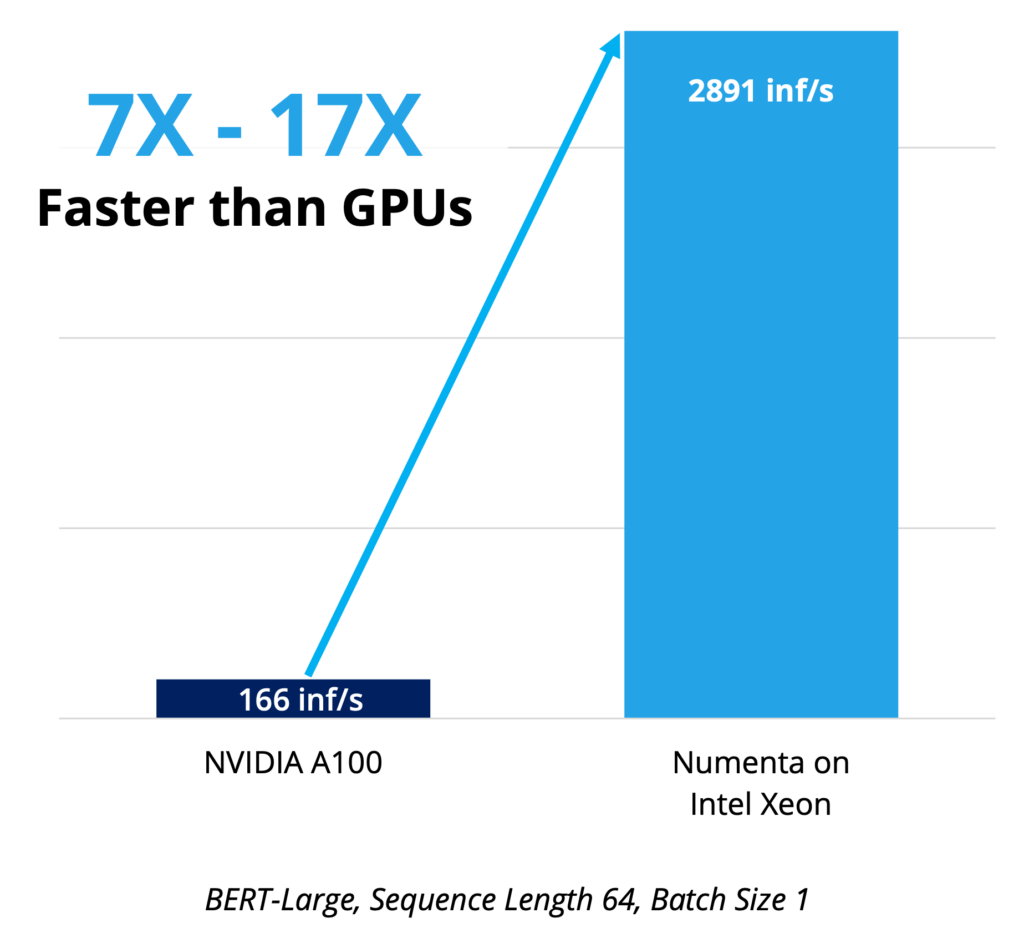
Numenta + Intel achieve 123x inference performance improvement for BERT Transformers
Numenta technologies combined with the new Advanced Matrix Extensions (Intel AMX) in the 4th Gen Intel Xeon Scalable processors yield breakthrough results.
